X射线应力测定方法

一、 确定测试方法的依据

    当接到一项X射线应力测定任务时，我们该从哪些方面来准备和考虑，以便正确选择测试方法和工作方案呢？
    首先应当熟知X射线应力测原理。为此必须事先了解X射线本质，具备必要的晶体学知识，懂得X射线衍射原理。
    其次，应当尽可能详尽地了解被测对象。知道了它的化学成分、组织结构和其中一些主要相的晶体学参数，才能够确定测量材料中哪个相的应力，进而选择衍射晶面、辐射和滤波片，查找或计算应力常数。知道了它的工艺历程和最后状态，特别表面状态，再进一步判断它是否存在织构，晶粒是否粗大，或者晶粒是否碎化（嵌镶块化），才能确定测量方法和条件。
    第三，在实际工作中常常会遇到实验的委托者并不了解X射线法测定的是指定点指定方向应力这一特点，只是笼统地要求测定工件的应力。在这种情况下，我们应当根据上述已知的信息，再加上工件的形状、尺寸等等因素，分析残余应力产生的各种可能的原因，初步判断工件各个部位应当是什么应力状态，这种应力状态对工件的使用性能或工艺性能有何影响，做到心中有数。在此基础上才能够确定测试部位、测点分布、应力方向、测试点的大小等等。还要依据试样的现有状态和测试目的，正确进行测试点的表面处理，并考虑是否需要和允许进行剥层，测定应力沿层深的分布。只有这样，我们最后提供的测试结果才是可信的和有价值的。

二、测量方法

1.X射线应力测定的基本思路

    依据布拉格定律2dsinθ = nλ，测定衍射角2θ，便可以计算出衍射晶面间距d 。假定被测材料为晶粒不粗大、无织构的多晶体，在一束X射线照射范围内应该有足够多的晶粒，而且所选定的（h k l）晶面的法线在空间呈均匀连续分布。如图1（a）所示，我们按倾角大小依次确定晶面法线ON0、ON1……ON4，通过衍射可以分别测定对应于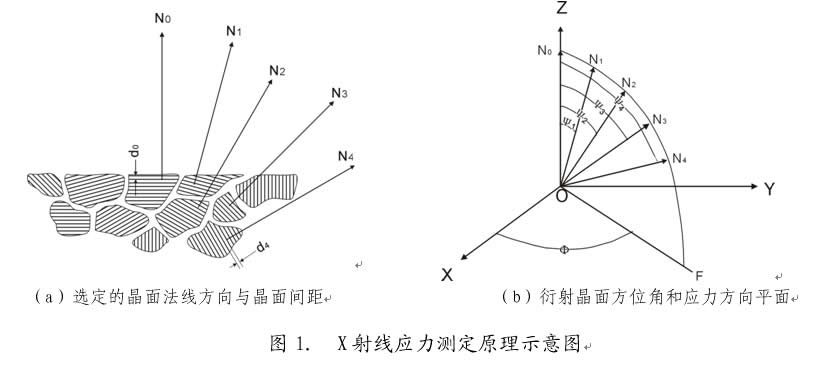这组法线的晶面间距d0、d1……d4 。容易看出，如果这些晶面间距在测量误差范围内是相等的，表明材料中无应力；如果d0、d1……d4依次增大，表明存在拉应力；相反，如果依次递减，则表明存在压应力。令衍射晶面法线与试样表面法线之夹角为Ψ，并称之为衍射晶面方位角，则图1中对应于法线ON0、ON1……ON4的衍射晶面方位角Ψ分别等于0、Ψ1……Ψ4 ，如图1（b）。这样又可以说，晶面间距d随着晶面方位角Ψ增大而递增或递减就表明材料表面存在拉应力或压应力，自然，递增或递减的急缓程度就反映了应力值的大小。
    根据布拉格定律和弹性理论可以导出所谓sin2Ψ法的应力测定公式：
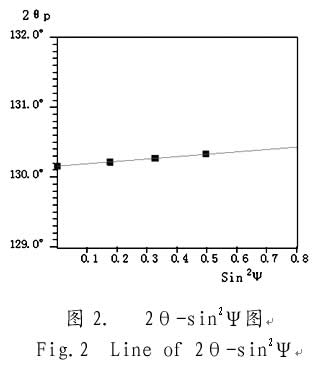
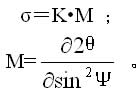              式中σ为应力值，K为应力常数，2θ为对应于各Ψ角的衍射角测量值，M即2θ对sin2Ψ的变化斜率（如图2所示）。由布拉格定律可知它反映的就是晶面间距d随衍射晶面方位角Ψ的变化趋势和急缓程度。这里2θ随sin2Ψ增大而增大，说明d随之减小，显然是压应力。
    这样看来，X射线应力测定的实质任务就是选定若干个Ψ角，测定它所对应的衍射角2θ 。完成这种任务的装置叫做测角仪，是X射线应力测定仪的测量执行机构。至此，我们应该明确了X射线应力测定的基本思路。
    应当指出，图1（b）中法线ON0、ON1……ON4所在的平面习惯上叫做Ψ平面，实际上就是应力方向平面，该平面与试样表面XOY的交线OF即为所测应力的方向。

2.固定Ψ法和固定Ψ0法

    图3是X射线应力测定的角度关系示意图。X射线从X射线管产生，经过入射光阑或准直管截取一束合适的光束照射到试样表面，设置X射线探测器，以照射点为中心进行扫描寻峰，测定衍射角 2θ。这就是最基本的衍射装置。入射线与试样表面法线的夹角叫做入射角Ψ0 ，而衍射角2θ指的是入射线的延长线与出现衍射峰时的反射线之间的夹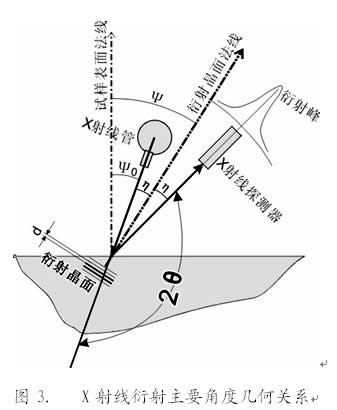角（下面的章节还要介绍确定衍射角的方法）。那么参加衍射的晶面应该处于什么方位呢？尽管晶面是微观的，根据入射角等于反射角的光学反射定律，我们却可以判定衍射晶面法线应当处在入射线与衍射线的角平分线的位置，它和试样表面法线之夹角Ψ即是衍射晶面方位角。
    按照寻峰扫描方式的不同，应力测定方法可分为固定Ψ0 法和固定Ψ法。
    固定Ψ0 法  上述基本衍射装置实现的就是固定Ψ0 法，其要点是在寻峰扫描过程中，入射线保持不动，即Ψ0 角固定，而探测器在一定范围内扫描。测定应力时需要设定若干个入射角Ψ0 （例如0°，15°，30°，45°），在每个Ψ0角都分别驱动探测器扫描求得衍射角2θ，然后计算应力。我们注意到设定的是Ψ0 角，而计算应力需要的是衍射晶面方位角Ψ ；如图3所示，

    固定Ψ0 法测角仪的机械结构比较简单，早期的应力仪多采用这种方法。而当前采用先进的固态线阵探测器或位敏固态闪烁探测器，免去机械式扫描的测角仪，其测量方法也应当属于固定Ψ0 法。
    但是，观察图3，设想探测器从衍射峰的起始角扫描到终止角，可以发现在这个过程中，接收的反射线与入射线夹角的平分线是在不断改变的，这就意味着参与衍射的晶面不断地有所改换。这样，对于晶粒较粗大或者存在织构的材料，衍射峰会产生畸变，影响应力测量结果[1,3,杨]。这便是固定Ψ0 法的缺陷所在了。
    固定Ψ法  固定Ψ法的特征是在寻峰扫描过程中，衍射晶面法线保持不动，即Ψ角固定；为此，入射线和探测器轴线必须等量相向（或相反）扫描，使得针对指定的衍射晶面法线而言入射角始终等于反射角。应力测定时直接设定若干个Ψ角（例如0°，25°，35°，45°），在每个Ψ角都进行这样的扫描求得衍射角2θ，然后计算应力。
    固定Ψ法严格遵循布拉格定律，物理和几何图像清晰，在扫描过程中参与衍射的晶面始终不改换，所以这种方法从原理上讲更为准确[1,3,杨]。显然对于织构和粗晶材料，只有采取这种方法才有可能得到较好的测量结果。
    实现固定Ψ法的途径又分为θ-2θ和θ-θ两种扫描方式。
    θ-2θ扫描方式是在同倾测角仪（如图4所示）上实施的。这种测角仪本来就是固定Ψ0 法的结构，X射线探测器及其驱动扫描的机构装置在固定X射线管的基体上。若要改变入射角，须驱动X射线管围绕照射点作圆弧运动；然而这个运动必然带动装在同一基体上的探测器作同步运动。为了实现固定Ψ法，在每个Ψ角上，于扫描起始的时候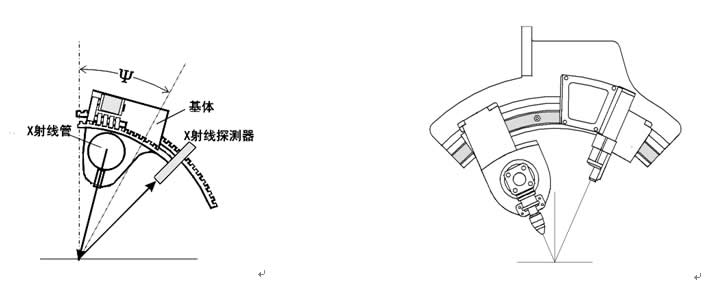，就必须将X射线管和探测器摆在以指定的衍射晶面法线为轴的对称位置上。在扫描过程中，当驱动X射线管并带动探测器运动一个“θ”角（例如0.1°）之后，接着再单独驱动探测器向相反方向运动一个“2θ”角（0.2°），这样就相当于二者各走一个“θ”角（0.1°）仍然保持对称的状态，使衍射晶面法线方向不变，在此刻接收反射的X射线。以后每一步扫描都是这样进行：θ，2θ，接收，θ，2θ，接收……这就是所谓的θ-2θ扫描方式。应当说明，在X射线应力测定仪上，这个扫描过程是依靠程序控制实现的。
    θ-θ扫描方式是在全新构思的θ-θ扫描Ψ测角仪上实现的。这种测角仪2θ平面（如图5所示）的特点是X射线管和X射线探测器分别安装在同一圆弧导轨的两个滑块上，对称分布，通过一套特别的传动机构实现同步等量相向而行，严格满足固定Ψ法的几何关系。

3.同倾法与侧倾法

    当一束入射 X 射线照射到多晶体材料上，以满足布拉格定律为条件，衍射线会形成一个以入射线为轴的衍射圆锥（如图6所示），横截圆锥便得到德拜环。圆锥上每一条母线与入射线之夹角都是衍射角 2θ（此时还应该想象到，在这个圆锥以内还存在一个衍射晶面法线圆锥，其圆锥角应是前者的1/2）。这样在进行应力测定时，2θ扫描平面的安置就有了一定选择性。首先设置入射线运动平面（Ψ0平面）垂直于试样平面，且与试样平面相交于 OX 直线，则2θ扫描平面既可设为与Ψ0平面重合，像图6（a）那样，也可设为与Ψ0平面垂直，如图6（b）所示。在X射线应力测定方法中，前者叫做同倾法（其含义是X射线管和探测器在同一平面内倾动），而后者称为侧倾法。

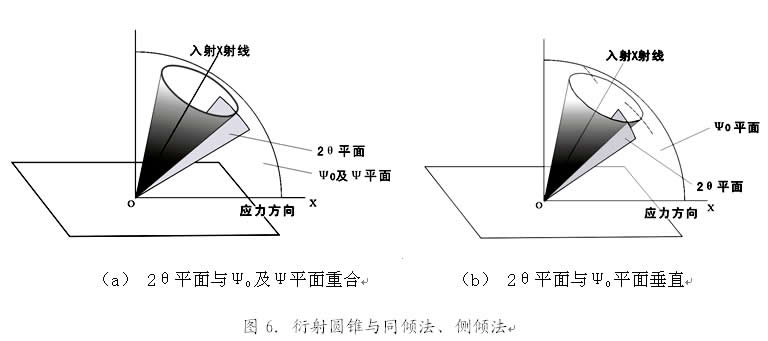
    在同倾的条件下，可以实施固定Ψ0 法，也可以实施固定Ψ法。在这两种方法中Ψ角都处于Ψ0平面之内。
    现在让我们留意刚刚提到的侧倾法。观察图6（b），固然Ψ0平面垂直于试样表面，然而处于入射线与衍射线角平分线位置的衍射晶面法线却不在Ψ0平面内，它与试样表面法线构成的Ψ角也离开了Ψ0平面。当入射线在Ψ0平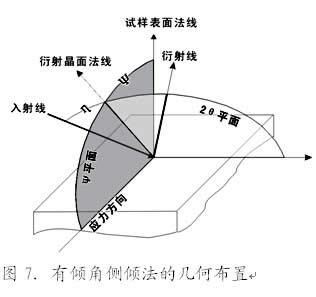面内运动时，衍射晶面法线并不在一个平面内运动，而且Ψ角的计算已不再简单。实际上，这种侧倾法应该叫做无倾角侧倾法，有专门的数学处理办法[2]。
    但是如果我们不把X射线管放在垂直平面内（如图7所示），而是让它在2θ平面内向探测器的另一侧偏过一个η角（η角见图3），则衍射晶面法线就恰好落在垂直平面内了。这样Ψ角就直观地等于2θ平面与试样表面法线之夹角。按照这种几何布置测定应力的方法叫做有倾角侧倾法。当然η角只能近似地用η0替代，η0由无应力状态的衍射角2θ0按（4）式计算而来。
    采用先进的固态线阵探测器或位敏固态闪烁探测器的测角仪，一般都可以选择侧倾法。但是，它的2θ平面通常由位于竖直平面内的入射线和对称分布其两侧的探测器组成。参看图6（b），相当于在现有2θ平面的另一侧增添了一个同样的2θ平面，二者在一个平面内，且垂直于Ψ0平面。显然，按照这样的布置，衍射晶面法线并不在竖直平面内，它相当于对称分布的两个无倾角侧倾机构的组合，只不过可以通过计算和修正求出正确结果。
    由图3不难看出，在同倾法的情况下，对于实际工件而言，2θ角与Ψ角往往存在测试空间上的冲突。即使对于平面试样，要使得Ψ0角大于45°，或者2θ角低于140°，就会出现难以克服的问题。而侧倾法的2θ平面为与Ψ平面相互垂直，就不存在这样的问题，因而可以扩大2θ扫描范围。从使用的角度来说，其优点[1,3,10]是：一、在某些空间受到限制的情况下，采用侧倾法显得比较有利；二、吸收因子与Ψ角无关，不必进行衍射强度的吸收校正；三、对于某些材料，如果在较高角度范围（140°～170°）无峰或峰形较差，则可以利用角度较低衍射峰。事实证明对于奥氏体不锈钢、铝合金、镍基高温合金、硬质合金等等材料，利用120°～140°范围内的衍射峰测定应力效果良好，显著提高测量精度。此外，X射线的穿透深度随Ψ角的变化较小，对表层具有较高应力梯度的试样特别有利；测定圆弧表面切向应力时，可得到较好的结果[3]。在学者的建议[1]和推动下，1998年我国研制出侧倾测角仪（Ψ测角仪）。
    但是，同倾测角仪还会有它一定的应用场合。由于它结构简洁轻巧，在某些情况下更加方便于携带到现场进行测试。实际经验还表明，在直角焊缝及其热影响区的应力测定场合，结构非对称的、使用短阳极X射线管的同倾测角仪发挥着独到的作用。

4.侧倾固定Ψ法
  
    如上所述，侧倾法与同倾法相比具有诸多优越性，固定ψ法实用效果又好于固定ψ0法；那么将侧倾法和固定Ψ法结合起来，即侧倾的条件下实施固定Ψ法（如图8所示），不但具有两者已有的全部优点，还会产生一个新特点──吸收因子恒等于1 [3]。这就是说，不论衍射峰是否漫散，它的背底都基本上不会倾斜，峰形对称性好，而且在无织构的情况下峰形及强度不随Ψ角而变化。显然这个特点对提高测量精度是十分有利的。从这个角度讲，侧倾固定Ψ法应该是最理想的测量方法 。采用θ-θ扫描Ψ测角仪可以直接实现这种方法。
 
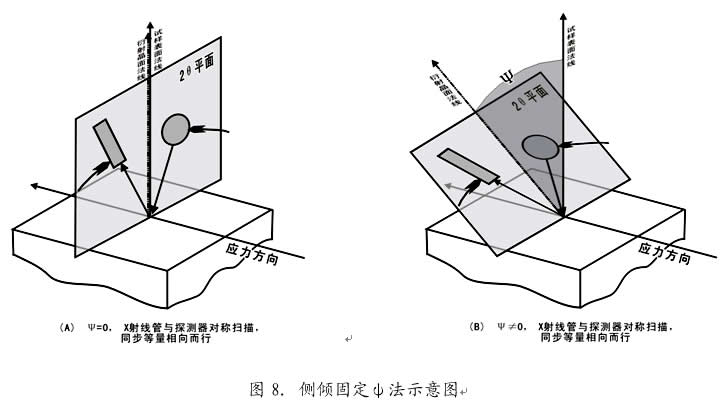
这里列举几个例子：
    （1）、测定奥氏体不锈钢的应力，采用CrKβ辐射，（311）晶面衍射，衍射峰在149.6°。在使用同倾法的时候，本来峰背比就比较差，加上吸收因子的作用，Ψ0=45°的衍射峰背底严重倾斜，往往无法确定背底，以致定峰精度很差。如果采用侧倾固定Ψ法，其结果是对应于各个角的衍射峰背底均不倾斜；如果材料晶粒不粗大，也无明显织构，则这些衍射峰的线形也都会比较完好，各峰强度无显著差异。这样，应力测定就会得到令人满意的结果。
    （2）、对于铝合金材料，采用CrKα辐射，（222）晶面衍射，衍射峰在156.7°左右，一般的同倾测角仪都可以测试。但是，这种材料往往晶粒较为粗大，并且可能存在一定织构度，所以测得的2θ-Sin2Ψ关系与直线偏离较大。实验证明同样的铝合金材料，（222）晶面织构度较大，而（311）晶面织构则可能相对较弱。采取侧倾固定Ψ法，仍使用CrKα辐射，在139.5°出现（311）晶面的衍射峰。实验表明，这样测试精度较高，即使对于要求应力水平必须很低的导航用陀螺零件，其测量结果也能满足控制生产工艺的要求。
    （3）、近年来材料表面的金刚石镀膜的残余应力备受关注。使用θ-θ扫描Ψ测角仪，CrKα辐射（220）晶面，衍射峰出现在130°，尽管应力常数高达－3374MPa/度，测量结果可信度仍然很高。

5.摆动法

    对于粗晶材料，在有限的X光照射区域以内，参与衍射的晶粒数目较少，衍射晶面法线在空间不呈均匀连续分布，因而衍射强度较低，峰形较差，难以达到应有的测量精度。另一方面，因为参加衍射的晶粒数过少，在衍射晶面法线方向上，他们的第Ⅱ类内应力之和可能不等于零，这也会影响残余应力的测量结果[3]。此外，如果X射线照射面积太小，也有类似的效应。研究表明[3]，有效衍射晶粒数目（进入计数管窗口有效面积内的衍射斑点数目）neff小于70时，neff对应力测量结果影响很大。nef与照射面积、接收狭缝大小和材料的晶粒度有关，可以计算出来。判断晶粒是否粗大还有比较简便的办法：在固定Ψ的条件下，改变X射线照射位置，如果所得衍射线形差别明显，净峰强度之差超过20%，就可以判定是粗晶材料。
    为了解决粗晶材料的应力测定问题，除了采用固定Ψ法以外，还可以考虑在允许的情况下增大照射面积，尽量选用多重性因子较大的晶面等措施。如果仍不奏效，就需要选择摆动法[1,10,11]。
    摆动法的要点是这样的：以步进扫描的θ-θ扫描Ψ测角仪为例（参看图8)，在扫描过程中，每一步都在保持接收角2θ不变的条件下，使2θ平面（连同X射线管）以指定的Ψ方向为中心，在Ψ平面内左右摆动一定的角度ΔΨ，在此摆动过程中计数。这里讲的是目前常用的固定Ψ加摆动法。其实在同倾和侧倾的条件下都可以摆动。在不同型号的应力以上，还会有固定Ψ0加摆动法，以及沿德拜环摆动法。
    摆动法的实质是把相应于Ψ±ΔΨ这样一个角度范围的衍射峰相叠加[11]，近似地当作指定Ψ角的衍射峰，客观上增加了参与衍射的晶粒数，把一些衍射强度较低而且峰形较差的峰叠加成为较为丰满、较少波动的峰，从而提高了粗晶材料的应力测量精度。

三、 定峰方法及其它数据处理

    如前所述，X射线应力测定的关键是准确测定衍射角2θ 。然而仪器直接测得的是衍射强度 I 沿接受角 2θ的分布曲线，即所谓衍射峰。在计算机控制的步进扫描或使用位敏探测器的情况下，直接测得的是 I-2θ坐标系中的一系列“点”。衍射强度是随机变量，尽管这些点按照一定的峰形分布，但是总会伴有一定的随机波动。那么如何由这些点求出满足布拉格定律的衍射角2θ呢？这就是所谓定峰问题，是数据处理中头等重要的一环。
    在X射线衍射分析技术发展过程中，先后形成几种得到公认的定峰方法，例如半高宽法，抛物线法，重心法等等，还有确定峰位差的交相关法。各种方法都是人为制定的，不能肯定那一种方法更正确，但是却可以说在各种不同情况下哪一种方法更合适。
    定峰之前还要进行背底处理、强度因子校正等，定峰之后则要作应力值计算及误差分析。

1、 背底处理

    衍射峰的背底是一些与测量所用的布拉格衍射无关的因素造成的，其中包括康普顿散射、漫散射、荧光辐射等等，这些因素都受吸收的影响，有的强度还随sinθ/λ值的增大而增大。所以扣除背底是提高定峰和应力测量准确性的必要步骤之一。
    研究表明，背底是一条起伏平缓的曲线，可以用一个三元一次方程描述[3]。通常都倾向于把它当作一条直线对待，实验证明这样的近似处理对于现行的测量准确度要求来说是可行的。为了扣除背底，首先要合理选取扫描起始角和终止角，使衍射曲线两端都出现一段背底。一般扣除背底的做法是这样的：在曲线的前后背底上，从两个端点开始，分别连续地取若干个（不少于5个）点，然后将这些点按最小二乘法拟合成一条直线；接着将所测得的衍射峰各点的计数减去该点对应的背底强度，即得到一条无背底的衍射曲线（如9图所示）。

2、强度因子校正

    根据X 射线衍射强度理论，与接受角2θ及Ψ角有关的强度因子包括洛伦兹-偏振因子LP（2θ）、吸收因A（2θ,Ψ）以及原子散射因数f（sinθ/λ）、温度因子e -2D 等。为了正确求得仅与晶面间有关的衍射角2θ，应当进行强度因子校正，这也是提高定峰和应力测定准确性的必要步骤[12]。计算表明，在应力测量用到的2θ范围以内，原子散射因数和温度因子随2θ变化很微小，可以忽略不计；而洛伦兹-偏振因子LP（2θ）尽管影响峰位，却与Ψ无关，所以在应力测定中也可以不加考虑；这样，最主要的就是吸收因A（2θ,Ψ）。所以在实行同倾法时计算程序中要加入吸收因子校正。但是如前所述，侧倾固定Ψ法吸收因子恒等于1，就无需校正了。

3、半高宽法定峰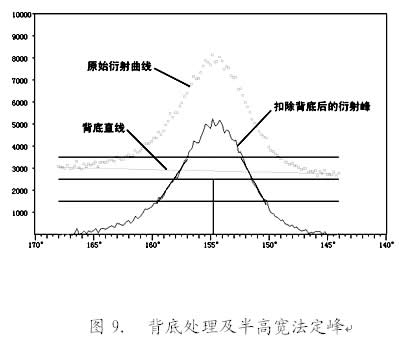

    半高宽法，就是把扣除背底的衍射峰最大强度1/2处峰宽中点所对应的 2θ作为峰位。一般计算软件所依据的数学模型如图9所示。其要点是把净峰高的两个“峰腰”部分当作直线，并用最小二乘法加以拟合；在净峰值强度 1/2  处作平行于横坐标的半高线与这两条峰腰直线相交；然后在两个交点之间取中，这个中点的横坐标值即是所求的峰位。上述的峰值强度亦非随机的最大值，而是峰顶拟合抛物线顶点的高度，这样可以减少随机误差。
    这种方法利用衍射曲线斜率较大的“峰腰”段进行计算，在这两段里，衍射强度的随机波动对峰位的影响较小，所以定峰精度较高。但是它要求设定足够宽的扫描范围，以保证得到曲线的前后背底。

4、抛物线法定峰

    抛物线法是把衍射峰顶部（峰值强度80%以上部分）的点，用最小二乘法拟合成一条抛物线，以抛物线的顶点的横坐标值作为峰位的定峰方法（如图10所示）。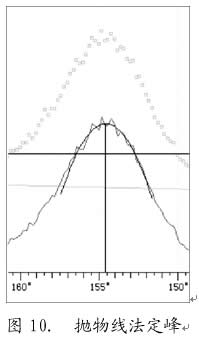
    这种方法利用峰顶部分进行计算，所以在对被测材料的衍射曲线形态比较熟悉的前提下，有可能缩小扫描范围，从而缩短测量时间。具体做法是这样的：首先选定充分的扫描范围测试一次求出背底，作为“公用背底”[3]，用于同一试样其它点或同种材质同样状态的其它试样的背底处理。后来的测试可以大幅度缩小扫描范围，只要能保证得到各个Ψ角衍射峰的峰值80%以上部分，就能正确进行定峰。当然应当注意保持 X管高压和管流的一致性，选用的准直管也应当是一样的。
    对于同一条衍射曲线，采用抛物线法和半高宽法得到的峰位不会相同，由于Kα1与 Kα2衍射峰并存，一般半高宽法峰位略高于抛物线法峰位（对比图9与图10）。在同倾法的情况下，由于衍射的几何原因，不同Ψ0角的衍射峰，其Kα1峰与 Kα2峰的叠合程度会有差异。因此即使对于无应力试样，用抛物线法得出的峰位亦随Ψ0角的增大而有所偏高，应力偏于负值。另外在照射点较小（或晶粒稍粗大）且接收狭缝较小的情况下，Kα1峰与 Kα2峰可能发生分裂，不宜采用抛物线法定峰。当然事先做分峰处理，再用抛物线定峰，那样就无懈可击了。

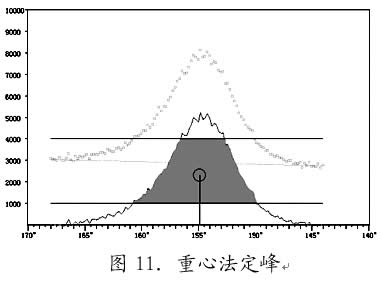5、重心法定峰

    重心法本来是以背底线以上整个衍射线所包围的面积的重心所对应的2θ作为峰位的定峰方法，物理概念很清晰，测试数据利用率也很高。但是实际应用效果并不理想。其原因在于峰两侧尾部的计数波动，虽然此处净强度不大，但是由于距重心较远，即杠杆臂较长，计算时对重心有一定的影响[1]。根据李家宝建议，截取净衍射峰的峰值20%至80%之间的部分，将之视为一个封闭的几何图形（如图11所示），求出这个几何图形的重心作为峰位，这样便显著改善了重心法的实用效果。

6、交相关法确定峰位之差

    交相关法（Cross-correlation method ）提出来的年代比较早[4]。但是由于这种方法涉及大量的、数量级很大的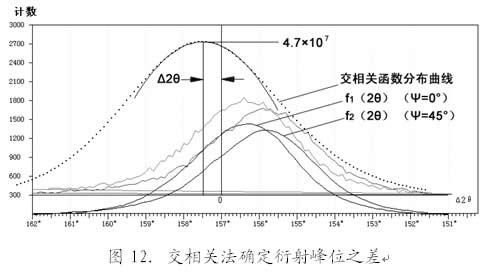计算工作，在计算机应用未能普及的年月是无法推广的。
    确切地说，交相关法计算出的是属于不同Ψ角的衍射峰位之差。这正是应力测定所需要的。图12所示的是一个实际测量结果。
    设Ψ=0°衍射曲线为f1（2θ），Ψ=45°的衍射曲线为 f2（2θ）。交相关法的思路是这样的：构造一个交相关函数F（Δ2θ），使每一个F值等于f1（2θ）、f2（2θ）两条曲线对应点的计数相乘而后全部相加所得之和；只不过在f1（2θ）与f2（2θ）相乘时，每一次f2（2θ）的自变量2θ都要改变一个扫描步距角δ，即   
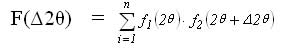           式中n为步进扫描总步数，这里的Δ2θ表示依次变化的整数k乘以步距角δ，即
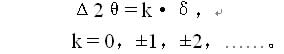显然F（Δ2θ）是Δ2θ的函数。f2（2θ+Δ2θ）的含义是把曲线整体平移Δ2θ。当Δ2θ= 0 时，即Ψ= 45°的衍射曲线不作偏移（k = 0），按（5）式计算得到的交相关函数F（Δ2θ）未必是最大的，除非应力为零，两曲线峰位完全重合；当Δ2θ恰等于两曲线峰位之差（我们欲求的峰位移）时，即人为地使两曲线峰位完全重合，则F（Δ2θ）必是最大值。反过来说，按（5）式计算，从正到负连续改变Δ2θ（即k=0，±1，±2，……），可以得到一条交相关函数 F（Δ2θ）分布曲线（如图12所示）。然后利用最小二乘法将这个分布曲线的顶部作二次三项式拟合，便可求得该曲线极大值所对应的横坐标值Δ2θ——我们欲求的峰位移。
    交相关法利用全部测量原始数据进行运算，每一个交相关函数值F（Δ2θ）都是大量数据相乘再加和的结果（其峰值比衍射峰高出4～5个数量级），无疑每个原始数据的随机误差相比之下变得极为渺小，因此这种方法定峰精度比较高。实验证明[5]，对于比较漫散的衍射峰，可以显著提高应力测量重复性。
    但是，这种方法要求作交相关处理的两个衍射峰形态相近似。如果被测材料因为织构、粗晶等原因致使峰形发生不规则的畸变，或者因为材料由多相组成，所选用的衍射峰近旁还有其它相的峰与之叠加，采用这种数学处理方法就不合适了。

7、应力值的计算及误差分析

    用此前计算出的各组峰位 2θ和  sin2ψ值，依据（2）式可计算出斜率M ；再乘以应力常数 K ，即得应力值σ （MPa）。计算斜率M利用最小二乘法，
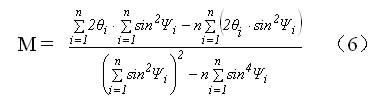                   式中n为测定应力选用Ψ角的数目。为简化起见[6]，令

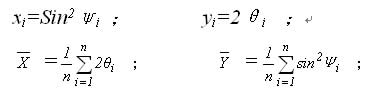
则（6）式变为
                             

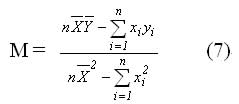
于是2θ-Sin2ψ的拟合直线可以表达为
                                
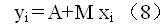
式中A为拟合直线在2θ-Sin2ψ图纵坐标上的截距，即Sin2ψ=0时对应的2θ，
                                 
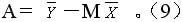
理论上 2θ和Sin2ψ成直线关系，然而测试所得的点与由它们拟合而成的直线之间，总会有或大或小的偏差，即存在一个拟合残差问题。应力误差 Δσ即反映了拟合残差的大小，                                 
                            
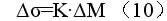
式中K为应力常数；ΔM 为2θ- Sin2ψ直线斜率的误差，按（11）式计算：

                     
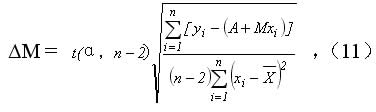
式中t(α,n-2)为对应自由度（n-2），可信度（1-α）的t分布值。
作为实例，图13提供三种实际测量结果，它们的误差大小各不相同。这里有两种情况：
第一，在材料中无织构的情况下， Δσ是由各种随机因素造成的，它是测量精度的表征。图13（a）的测量误差很小。图13（b）的误差则稍大；通常通过改善测量条件，还可以减小这个误差。因为随机误差的主要应影响因素是衍射强度（或各点总计数）；其次是衍射峰的半高宽。形象地讲，峰形敏锐，则误差小；反之，峰形漫散，则误差大。经过实验与分析，在连续扫描条件下衍射角误差Δ2θ与有关参数之间存在如下回归关系[7]：
                  
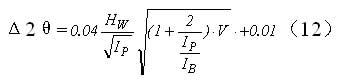
式中 
HW——衍射峰半高宽（°）；
Ip——净峰强度；
IB——背底强度；
V ——计数管扫描速度 （°/min）。
    第二，如果出现图13（c）那样的情况，2θ和 Sin2ψ已不再是直线关系，可以认为Δσ除包含测量偶然误差以外，更主要的可能是存在织构或晶粒粗大所致。

四、衍射几何问题

    从衍射几何来说，在X射线衍射仪上测定应力通常采用聚焦法或准聚焦法。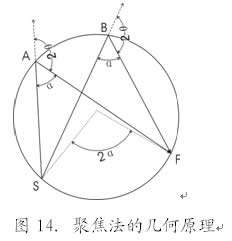
    聚焦法的原理十分简明[8]。如图14所示，发射点S、被照射弧面AB与接收点F同处一个圆上，根据对同一圆弧的圆周角相等的定理可知，由S点发出的X射线照射到A至B，而A至B所有的衍射线均以相等的衍射角2θ聚焦于F点。
    日本学者在研制应力测定的专门衍射装置时，采用了平行光束法（如图15）。它的X射线管的投影焦斑（X光源）约为4×4mm的矩形，入射和接收光阑里都按等间距装置了隔片，这样可以认为入射线大部分为平行光。
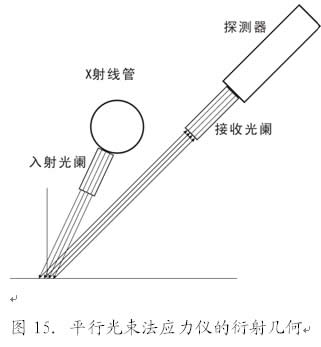    分析和实验结果都表明，采用平行光束法，对测角仪至被测点距离（Y）的设置误差（ΔY）宽容度比较大，在ΔY不超过±3mm的情况下，它所造成的衍射角的测量误差不会超过±0.03°[3]。这一特点客观上起到提高测量精度的作用。对于表面应力分布梯度不大的试样，容许一定的设置误差ΔY，还能保证测量精度，这给实际测试工作带来方便。但是如果分布梯度比较陡峭（例如测定焊接应力在垂直于焊缝方向上的分布时），设置试样时一旦有了可以察觉的ΔY，则不同Ψ角时X光照射位置就会有所不同，这样的测量就无意义了。另外在需要限制照射面积的时候，假若只有一两个隔片中的狭缝通光，那样就和准聚焦法没有明显区别了。还有，平行光束法的衍射强度和分辨率都比较低，这是它显而易见的缺点。
    上世纪八十年代中期，汲取国内专家的研究成果[9]，国产X射线应力测定仪采用了点焦斑X射线管和准聚焦法的衍射几何，其光路系统示如图16所示。当入射角Ψ0一定时聚焦圆就固定了，探测器不沿聚焦圆扫描而是沿着测角仪圆扫描；另一方面，被测试样表面通常与聚焦圆并不吻合；因而叫做准聚焦法。但是仔细分析起来，如图17所示，在试样被测点为平面的的情况下，聚焦圆上的衍射强度分布倒不如测角仪圆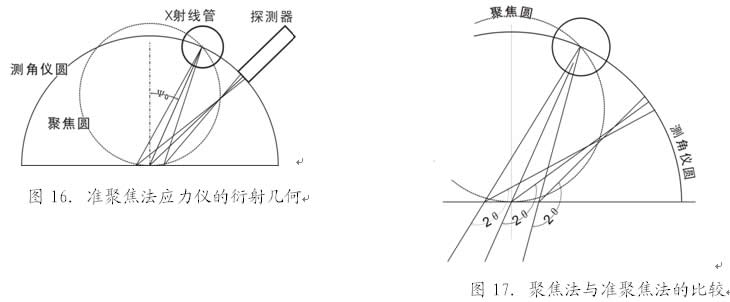上的分布更合理一些[1,9]。实际应用结果表明，准聚焦法在提高衍射强度、减小测量误差方面收到了良好效果。
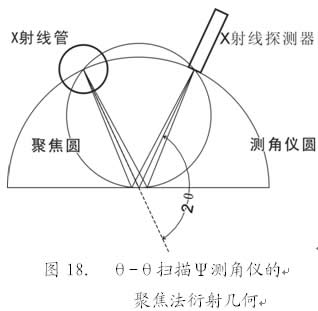    如前所述的θ-θ扫描Ψ测角仪的衍射几何属于聚焦法，图18是这种测角仪的光路示意图。这里虽然也有不符合严格聚焦条件之处，例如X射线管虽然是点焦斑，但光源不是几何意义上的点，总有一定的大小（0.5×0. 5mm），试样被测点表面与聚焦圆不可能完全吻合；但是在X射线管和探测器沿测角仪圆对称扫描的过程中始终处于同一个聚焦圆上，实属难得的特点。容易看出聚焦圆直径是不断变化的，2θ越低则聚焦圆半径越大。
    聚焦法的优点是衍射强度和分辨率比较高，在一定限度内增加入射光束发散度对衍射峰半高宽无明显影响。它的缺点是对测角仪到被测点的距离的设置要求比较严格。但是现在已有了精确设置试样的手段，控制设置误差已经比较容易，因而推广使用聚焦法是可行的。

五、  辐射、衍射晶面与应力常数

    5.1 辐射和滤波片
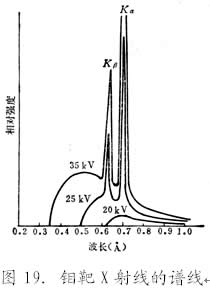
    X射线管发射的X射线分为连续谱线和标识谱线（如图19所示）。X射线衍射分析使用标识X射线。当X射线管电压达到并超过靶材的激发电压VK 时，来自阴极的高速电子具有了充分的动能， 能够撞出靶原子内层（例如K层）电子而产生空穴，原子处于激发状态，外层（例如L、M层）电子遂向空穴跃迁，以使原子恢复常态；跃迁电子的能级之差以X光量子的形态辐射出来，便是标识X谱线。其频率υ与能级之差E1－E2成正比，
             
h为普朗克常数。若用X射线波长λ表达，则
                
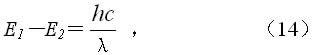
式中c为光速。同一系（例如K系）标识谱线，其波长λ取决于靶材原子序数Z，它们之间的关系符合莫塞莱定律：
              
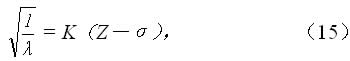
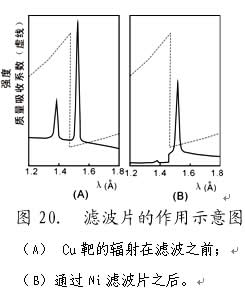式中K和σ均为常数。所谓标识谱线，其含义就在于它的波长与靶材原子序数的一一对应的关系。因靶原子K层出现空穴而产生的X射线叫K系谱线，L层电子跃迁到K层空穴所产生的X射线叫Kα辐射，M 层电子跃迁到K层空穴所产生的X射线叫Kβ辐射（如图19所示）。所以，选择不同波长的辐射就是选用不同靶材的X射线管，或同一靶的不同辐射。
    在选用Kα辐射的情况下，为了突出其单色化效果，提高衍射线的峰背比，应当设法滤除Kβ辐射，并降低连续谱线的强度。为此就要在光路中加装滤波片。
    滤波是吸收缘效应的巧妙利用。所谓吸收缘效应，即在材料对X光的质量吸收系数μm随入射X光波长λ而变化的曲线上有一个突变缘（如图20虚线所示），波长大于此缘时质量吸收系数μm已经变得很低，小于此缘时μm陡然增高。实际上，这是因为波长等于吸收缘的入射X光所具有的能量恰能撞出被射物质原子内层电子，并引起电子跃迁，产生二次X射线，故而被射物质对入射X光显现出强烈的吸收，这又被称为真吸收。
    面对图19我们不妨设想，如果某种材料的K吸收缘恰好位于入射的Kβ辐射与Kα辐射之间，不是正好可以利用它滤除Kβ辐射吗？事实正是如此，只要滤波片材料的原子序数比X光管靶材小1或2，就可以实现这个巧妙的设想，如图20所示的那样。
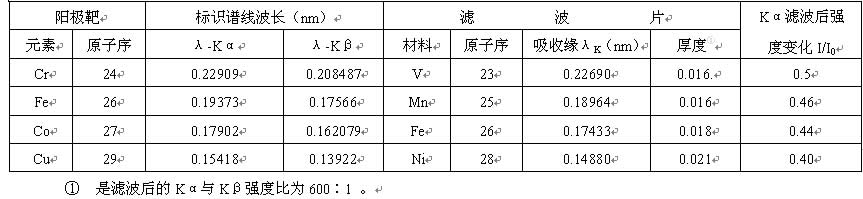
    X射线应力测定常用辐射及滤波片的有关数据见表1。

表1.  不同X射线管所用的滤波片

   
5.2 衍射晶面的选择
    选择衍射晶面的根本依据是布拉格定律：
                                        2d sinθ= nλ 。
    当然事先要知道现有仪器提供的前提条件：一是仪器配置了哪几种靶材的X射线管，它决定了有哪几个波长λ的辐射可以选用；二是测角仪的2θ范围。
    晶面指数(h k L)表征了晶面相对于晶体点阵坐标的取向。它的数字越小，其上的原子密度越大。为了得到较大的衍射强度，应当尽量选用指数较小的晶面作为衍射晶面。但同时要依据布拉格定律，使晶面间距d与X射线波长λ适当配合，以便在仪器允许的范围内得到完整的有足够强度的衍射峰。
根据弹性力学和布拉格定律进行推导，可得应力常数的如下表达式：
                    
式中θ0为无应力状态的布拉格角。（16）式表明θ0越大则应力常数K越小。所以要尽量选用衍射角2θ比较高的衍射晶面。因为应力常数K越小，同样的衍射角2θ测量误差引起的应力值误差也越小。

    5.3  应力常数问题
    应力常数表达式（16）中的E和ν分别是杨氏模量和泊松比。应当指出，这里的E和ν应当是材料中指定相、指定晶面（ h k l）应力应变关系的参量。在多数情况下这里的E和ν与机械法测得的多晶材料的E和ν在数值上有很大差别。而且一般材料的这些参量对合金元素含量及组织结构不敏感，但是（16）式中的E和ν不仅与晶面指数有关，而且与材料的成分、塑性变形历史以及热处理状态等因素有关。所以如果要追求与载荷应力完全一致的残余应力值，可以采取实验手段测定应力常数。
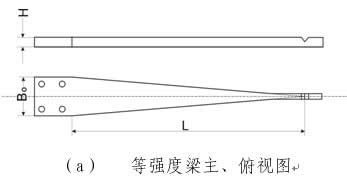    为此，用与待测应力工件的材质工艺完全相同的材料制作成等强度梁，如图21（a）所示。右端“V”型槽处于两条斜边延长线的交点上。图21（b）是等强度梁加载装置示意图。如果载荷为P，则等强度梁上面的载荷应力σp按下式计算：
           
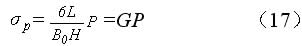
式中G称作等强度梁系数（这里提供一个参考尺寸：L=300mm，B0=50mm，H=6mm，计算得G=1）。
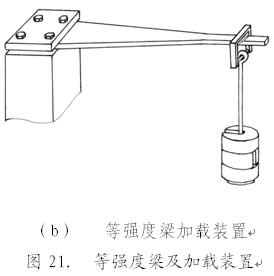    测定应力常数的办法是这样的：给等强度梁施加一系列不同的载荷Pj，在每个载荷下，分别用X射线应力测定仪在等强度梁上面测定衍射角2θ对sin2Ψ的斜率Mj （操作方法与测定应力相同）：

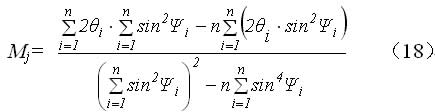
式中n为测定斜率选用Ψ角的数目。测试点应当确定在梁的中心线上远离边界条件的某一点，应力方向与中心线一致。假定测试点的残余应力为σr ，则载荷应力与残余应力的代数和σpj +σr应与X射线应力测定所得的斜率Mj成正比，即
                              
一般地表达，
                                                   
式中σr和K为未知数。这是个直线方程，K为直线的斜率。对（20）求导，得 
                             
由一系列的载荷应力σpj和实测数据Mj ，用最小二乘法可以求得应力常数K ：
                           
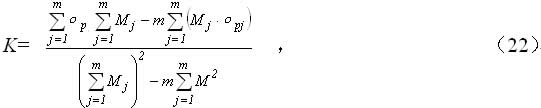
式中m为等强度梁载荷系列中的个数。
    此外，也可以把材料做成板状试样，利用其它型式的加载装置，在试样上粘贴电阻应变片，同时用电阻应变仪和X射线应力测定仪（或衍射仪）测定应力常数[2 ]。
    实验测定应力常数是一项非常细致的工作。所以应当注意：一，等强度梁及其加载装置的制作与安装都必须保证足够的精度；梁体材料不但要和待测材料的材质状态完全一致外，还要注意避免晶粒粗大和织构，并且注意去除机械加工带来的附加应力。二，作X射线衍射分析时应当严格把握应力方向、Ψ=0°状态的垂直度和标定距离；还要注意随着载荷增加等强度梁发生弯曲，每次都要校准距离和垂直度。
    关于理论计算X射线应力常数问题，前人曾提出不同的假设和计算模型[1]。文献[1]根据统计波动理论，推导出多晶体的弹性常数应取按Viogt和 Reuss两种假设计算所得结果的几何平均值，并在附录中列出了常用金属材料、一些陶瓷材料和硬质合金的应力常数，被国内外同行普遍采用。

六、  测量条件的选择

6.1 衍射强度问题与管电压、管电流的选择
    6.1.1 衍射强度问题
    衍射强度指的是探测器在某个接收角上单位时间内采集到的X光子数，也就是探测器单位时间内输出给计算机的脉冲数。衍射强度是随机变量，必然带有随机误差。从仪器制造的角度，提高X射线管电压、电流的稳定度和探测器的稳定性，可以减小衍射强度的随机波动，但是要想使它完全恒定是不可能的。
    多晶材料的衍射强度首先取决于原子散射振幅、晶胞的结构振幅、衍射晶面的多重性因子、单位体积内的晶胞数，还有角因子、吸收因子、温度因子等等因素。其次，材料的状态和组织结构也会影响衍射强度。晶体缺陷增多，原子排列的周期性有某种程度的下降，衍射强度必然降低。再者就是几何因素—照射面积大小和接收狭缝的影响。如果要求测定微小区域的应力，允许的照射面积很小，则衍射强度就会很低。
    在面临很弱的衍射峰时，为了使得应力测试结果具有足够的可信度，就必须设法提高衍射强度，或增大探测器累计的计数。因为计数越高，则它所包含的相对误差就越小。
    从另一个角度来说，衍射强度也给我们带来了被测材料的金属物理信息。对于相同的材料，在相同的衍射晶面和衍射几何条件下，一旦发觉衍射强度的明显变化应当引发我们的思考和分析。必要时再配合使用其它手段，寻求材料内部组织结构的特性，以及它们对材料性能的影响。
    6.1.2 管电压、管电流与X射线发射强度
    为了提高衍射强度，首先应当关注X射线发射强度。标识X射线的发射强度I标随着管电压V、管电流i的升高而增大，实验结果表明，
                         
    式中C为比例常数， VK为X射线管靶材的激发电压，m是个实验测定值，对K系，取m=1.5 。如前所述，标识谱是叠加在连续谱上的。管压提高，标识谱增强的同时连续谱也增强，而后者对于衍射分析是不利的。理论推导和实验都表明连续谱线的强度I连与管电流i及管电压V的平方成正比，
                          
式中K为常数，Z为靶材的原子序数。为了得到标识谱和连续谱二者最佳强度比，应当寻求最佳工作电压。由（23）式和（24）式可以导出I标 / I连 以（V/VK）为自变量的函数关系，并得到相应的曲线（图22）。该曲线表明，当管电压V为激发电压VK的3～5倍时，可以得到标识谱对连续谱的最佳强度比；其实达到2.5倍时已接近最佳。按此规律，常用X射线管的激发电压和适宜工作电压列于表2 。   
    6.2 入射光束张角与照射面积•接收光阑
    关于入射光束张角大小问题，上世纪八、九十年代多内外学者做了很多研究。在汲取学者们研究成果的基础上，目前国产X射线应力测定仪的θ-θ扫描Ψ测角仪在满足聚焦法的衍射几何条件的前提下，配备了直径分别为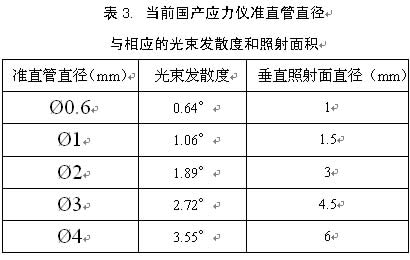Ø0.6mm、Ø1mm、Ø2 mm的准直管作为入射光阑，另配Ø3 mm、Ø4 mm准直管备选（表3），Ø4 mm用于特殊场合。前三种准直管对应的光束发散度分别为0.64°、1.06°、1.89°。大量实验证明采用这些准直管，应力测量系统误差均在允许的范围以内。Ø3 mm准直管对应的光束发散度时2.72°，在实际测量中也被经常使用，亦未见显著系统误差。进口的AST和TEC公司的仪器提供的准直管也有5种，分别产生直径为Ø 1、Ø 2、Ø 3、Ø 4和Ø 5mm的光斑。若从测量偶然误差角度考察，随着准直管直径的增大，X射线照射强度显著增强，从而使得应力测量精度随之提高。
    当然应当同时注意到，准直管直径越大，X射线照射面积也越大。操作者应当明确了解，测得的应力是X射线照射面之内的平均值。因此必须考虑被测试件的具体情况，合理确定照射面积的大小。首先应当根据产生残余应力各种可能的原因，分析它的大小在试件表面各处是否会有很大的分布梯度。原则上讲，梯度小则照射面积允许大一些（例如测定平面喷丸试件应力）；如果应力梯度比较大（例如测定焊接应力），则应当选用直径较小的准直管。其次，应当考虑被测工件的尺寸和形状；显然在小平面上或曲率半径较小的弧面上测试，必须选用直径较小的准直管。为了合理地增大照射面积，有时操作者还可以考虑使用狭缝式入射光阑。对于在一定方向上存在明显应力梯度的试样，让狭缝与这个方向垂直；对于小的圆柱或内圆弧试样，让狭缝平行于试样的母线。
    接收光阑装置在计数管（探测器）窗口之前，起到限制光束和屏蔽散射光的作用。当前国产应力仪配置的接收光阑狭缝有以下几种：1.8×6mm，0.9×6mm，0.36×6mm和0.18×6mm，在测角仪圆上对应的角度分别为1°，0.5°，0.2°和0.1°，通常采用1.8×6mm狭缝。不装狭缝片时接受宽度为3×6mm。接收狭缝越宽则计数率越高；选择较小狭缝在一定程度上可以提高衍射线的分辨率。
    6.3 Ψ角的选择
    GB7704-87规定按固定Ψ0法测定应力时，Ψ0角取0°、15°、30°和45°；而采用固定Ψ法时，Ψ角取0°、25°、35°和45°[4]。
    在实际测试工作中只取0°和45°两个Ψ角或Ψ0角的情况也比较普遍，因为这样工作效率比较高。但是这样做应当具备如下先决条件：材料具有良好的各向同性性质，织构不明显；X射线有效穿透深度以内应力梯度较小；晶粒不粗大；衍射峰比较敏锐，峰背比高，因而衍射角2θ测量精度比较高。在我们面对一个新的试样，不能确定它具备这些先决条件的情况下，一定要选取四个或四个以上的Ψ角进行测试，否则就无法确认测试的可信度。
    在选取的若干Ψ（Ψ0）角当中，最小的一般取0°，最大的应当尽量大一些，这样从应力计算的角度考虑可以提高测量精度；但是同时还要考虑其他因素。例如，在同倾法的情况下，如果Ψ（Ψ0）角太大，试样对反射X射线的吸收严重，使得衍射峰背底严重倾斜，势必影响定峰精度。在采用侧倾固定Ψ法的时候，吸收因子造成的影响不存在了，Ψ角可以适当加大；但是无论是侧倾法或是同倾法，如果最大的Ψ（Ψ0）角太大，对于各个Ψ（Ψ0）角来说，X射线穿透深度和照射面积差别也会变大，从而使应力测量结果的实际意义降低。
    四个或四个以上Ψ角的设置原则，通常是使它们在sin2Ψ坐标上具有大致相等的间距，这样每个衍射角2θ测量值对测量结果的计算能够起到同等的作用。
    在遇到形状比较复杂的工件，测试空间不允许设置足够宽的Ψ角范围时，即使满足上述先决条件，也应当在允许的范围内至少设置4个Ψ角，这样才能保证测量结果的可信度。
    6.4  半高宽问题与2θ扫描范围、扫描步距、计数时间
    按照布拉格定律，只有在严格的2倍布拉格角θ上才会出现衍射强度的极值，然而实际的衍射峰总会跨越一定的角度范围。为了描述这一现象，就用到了半高宽，即除去背底的衍射峰在其最大强度1/2处所占据的宽度，以度（°）为单位。从X射线衍射分析的角度来说，它是个非常重要的物理参数。它的大小既有几何因素，又有物理因素。几何因素指的是入射光束发散度越大，接收狭缝越宽，则半高宽越大。当然在聚焦法衍射几何条件下，入射光束发散度在合理范围以内的增大对半高宽影响较小。就物理因素而言，因塑性变形或相变致使晶粒碎化（嵌镶块化），第二类内应力（微观应力）增大，位错密度增高，都会导致衍射峰宽化。而这些因素往往会影响到材料的力学性能。
    正确设定2θ扫描范围的原则是在所设定的扫描范围内使得各个Ψ角都有完整的衍射峰。所谓完整衍射峰，就是具有前后背底的衍射曲线。更明确地说，按照第五讲的办法给衍射曲线确定背底直线之后，衍射曲线的前后尾部应当圆滑过渡直至与背底直线相切。实际上扫描范围应当根据衍射峰的半高宽来确定。经验表明， 2θ范围应当达到半高宽的4倍至4.5倍。除了半高宽以外还要考虑应力值的大小；应力较大时，顾及各Ψ角衍射峰的偏移，2θ范围还得适当加宽。
    2θ扫描方式分为连续扫描和步进扫描，后者又叫阶梯扫描。这里介绍的是如何确定步进扫描的步距和计数时间。采用固态线阵探测器则是多通道同时接收，由计算机的CPU瞬间依次扫描读取各个通道的计数，它的步距是固定的，也有计数时间问题。
    扫描步距就是阶梯扫描过程中探测器每次前进的角度。它的大小决定了衍射曲线上点的密度，亦即定峰时参与计算的数据点的多少。显然点数越多，测量结果的随机误差就越小。但是考虑到工作效率，又不能无限制地缩小步距。经验表明，半高宽在2°以下，步距角可以选择0.05°；半高宽在2°～4°的，一般取0.1°；半高宽在5°以上的，可以考虑用0.2°、0.25°等等。
    计数时间就是探测器扫描过程中每前进一个步距角之后停下来接收反射X光子的时间。就好像是照相机的快门，曝光时间越长底片感光量越大一样，计数时间越长，则探测器接收到的X光子数越多。为了达到满意的测量重复性，总是希望计数尽可能高一些。在衍射强度较低、峰形较差的情况下，应该考虑适当延长计数时间。但是峰形的好坏并非只取决于计数高低这一个因素，在某些情况下仅靠延长计数时间也未必能够达到理想的结果。相反，对于峰形较好的材料，有时候计数不高（例如峰值在1000以下）也能达到满意的测量结果。在这种情况下，计数时间可以缩短，以利于提高工效。

    综上所述，在指定材料和衍射晶面、确定照射面积的前提下，如果出现衍射强度较低，峰形较差，测量误差较大的情况，首先判定材料的晶粒是否粗大，是否应当采用摆动法。如果晶粒并不粗大，那么可以采取的措施包括：①提高管流管压；②延长计数时间；③增大接收狭缝；④缩小扫描步距。在实际操作中这些措施可以相互配合使用。

    七、 试样表面处理
    在X射线应力测定技术中，试样表面处理是关键问题之一。因为所用X射线一般不属硬射线，在金属表面的有效穿透深度通常为几微米至十几微米，测得的应力就是这个深度内应力的加权平均值。显然，试样表面状态对测量结果有决定性影响。原则上讲，表面光洁度越高，应力测定就越准确；粗糙的表面应力会有一定程度的释放。GB7704-87规定[4]被测部位表面粗糙度Ra应当小于10μm 。
    选择测试点应当尽量避开工件表面缺陷和磕碰划伤痕迹。采用适当的方法清除油污、氧化皮和锈斑，使测试部位露出洁净的金属表面，这是表面处理的第一步。这里应当注意尽量不使用坚硬工具，避免伤及原始表面。例如，去除油污可以使用有机溶剂，去除氧化皮可以使用稀盐酸等化学试剂。
    然后依据测试目的和测试点表面实际情况，正确进行下一步的表面处理。
    1、如果目的是为了测定各种机械加工（例如车削、磨削、喷丸强化、滚压强化等等）所产生的残余应力，就必须小心保护原始表面，不作任何有损原始表面的处理。当然为了探求应力和半高宽沿层深的分布，接下来还要做剥层。
    2、对于铸件，应当注意到表面激冷层和内部组织是有明显区别的，而且表面比较粗糙。但是，激冷层通常不存在织构，应力测定结果可信度较高。作为不同铸造工艺的对比实验，这些结果可能有它的参考价值。如果需要更准确地测定铸造应力，一般要对表面进行修磨；但是应当注意到应力值的大小沿层深会有一定的梯度，故而修磨深度必须严格控制，测量结果才有可比性。
    4、对于焊缝，一般要去除附加高，因为这部分表面与母材没有一致性力学关系，而且有焊波存在，表面不平整，无法测试。另外还要清除表面的焊疤、敲击痕迹和各种缺陷。一般总是在选定的部位，从焊缝中心到热影响区以至母材，打磨出连续平整的一片区域，测试点排列在这个区域之中。
    5、在采用锉刀、砂轮、砂布进行修磨，乃至进行机械抛光之后，必须采用电解抛光或化学抛光的手段去除修磨抛光带来的附加应力层。
    至于附加应力层的深度，因机械加工和修磨的方式不同而有区别。作为参考，这里提供如下数据：手工细砂纸磨光的影响深度一般在30微米以上，而机械磨削的影响深度则可能在150微米以上。为了准确可靠地去除附加应力层，可以在电解或化学抛光的过程中逐层测定应力，观察应力值和衍射峰半高宽的变化；当应力值达到稳定不变时可以认为已经去除了附加应力层；另外，机械修磨必然在某种程度上引起衍射峰的宽化，如果观测到半高宽逐层减小直至稳定不变，也可以认定已经去除机械修磨的影响层。
    这里还要注意以下事项：
    （1）砂磨过程应当由粗到细，逐级进行，最好的做法是按照现场金相检验的要求处理待测试部位，然后再作电解或化学抛光。
    （2）对于石墨和碳化物含量较高的铸铁材料，在作电解抛光时，到达要求的层深之前，用金相砂纸轻磨，或用绒布加研磨膏抛光，除去电解抛光面残留的石墨和碳化物，使之显露金属光泽，最后用较小电流密度作短时电解抛光。
    （3）抛光好的表面须及时清洗擦干，避免氧化和污染；更要小心加以保护，避免摩擦和碰撞。甚至在测量抛光深度时也要小心，因为量具留下的磨痕也会影响应力测量值。

八、 仪器的校验、调整与和试样设置

    当前不论国产还是进口的X射线应力测定仪，其最基本的构成（图23）应当包括：（1）作为测量执行机构的测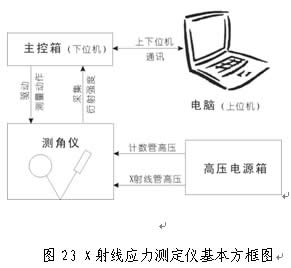角仪；（2）控制测量动作、采集数据的主控箱；（3）提供X射线管高压和计数管电压的电源箱；（4）用于选择条件、运行程序、下达指令、处理数据和输出结果的微电脑。测角仪上安装着X射线管和探测器，为了测定应力，它必定包括Ψ（或Ψ0）和2θ两套运动机构。采用固态线阵探测器的测角仪的2θ部分无需扫描动作，但是一般也会有人工改变探测器位置的圆弧机构。需要强调指出，这两套运动机构必须以同一点为回转中心，该点就是被测点的正确位置。这便是校验和调整测角仪的根本依据。
    按照计量管理规程，X射线应力测定仪应当定期校验。在较大规模的拆卸、搬运、重新安装之后也应当校验。校验测角仪须使用荧光屏和无应力粉末（例如还原铁粉）试样。荧光屏在X光的照射下能够发出可见的绿色光斑。
    第一步，在荧光屏上做刻线，放在被测试样位置，按照所用仪器规定的方法校准距离和方向。然后开启X射线，驱动测角仪的动作，分别在Ψ和2θ两个运动过程中观察光斑中心是否偏移。只有不存在肉眼可以察觉的偏移，光斑中心才可能是测角仪Ψ和2θ的回转中心，应力测量才可能是准确的。如果观察到了微小的偏移量，一般可以通过修正标定距离Y（测角仪至被测点的距离）的办法消除它。
    第二步，按照第一步校准的标定距离Y，测定无应力粉末试样的应力。如重复测试的结果在允许的误差范围（例如±20MPa）以内，则仪器可以判定为合格。
    第三，如果第二步的测量结果超出允许范围，而且反复测量证实为系统误差，说明上述第一步看到的光斑中心和测角仪Ψ、2θ真正的回转中心还有微小差距，只是由于几何原因，转动Ψ和2θ时用肉眼无法察觉光斑的偏移罢了。在这种情况下，可以微微调整X射线管的安装位置，使光斑向左或向右作微量移动，然后再重复上述第一步、第二步的操作，直至消除了不容许的系统误差，届时光斑中心和测角仪回转中心便真正地一致了。
    在上述第一步当中，观察X光斑必须注意X射线防护！当前国产仪器在测角仪上装置了微型激光器，用对人的眼睛无害的红色激光代替X光，给仪器的校验和使用带来方便。
    试样设置须注意以下几个方面：
    1、 应力方向。欲测定的应力方向应当平行于测角仪的Ψ平面。
    2、 标定距离。按照所用仪器规定的方法校准标定距离Y。对于聚焦法测角仪标定距离Y应当更严格掌握，误差ΔY不要超出±0.2mm。
    3、 Ψ角的准确性。对于θ-θ扫描Ψ测角仪来说，在其Ψ=0°状态，被测点表面法线应当与入射线和接收的衍射线夹角的平分线重合。而其他型式的测角仪，在其Ψ0=0°状态，被测点表面法线应当与入射线重合。为此，国产仪器配备一个“垂直验具”，配合激光使用；进口仪器也应该有相应的办法。

参考文献：
[1]  张定铨，何家文. 材料中残余应力的X射线衍射分析和作用. 西安交通大学出版社. 1999.4.第1版.
[2]  李仁文. 无损检测. 1979,1(5):41～46
[3]  李家宝，机械工程材料测试手册 物理金相卷（总主编桂立丰，卷主编唐汝钧，辽宁科学技术出版社，
沈阳，1999年11月第1版），第三篇，第7章。
[4] 中华人民共和国国家标准GB7704-87《X射线应力测定方法》.

参考文献：
[1]  张定铨，何家文. 材料中残余应力的X射线衍射分析和作用. 西安交通大学出版社. 1999.4.第1版.
[2] 金属研究所疲劳研究组，入射无负η倾角侧倾法X射线应力测定技术，金属学报，第13卷第1，2期，1977.6.
[3] 李家宝，机械工程材料测试手册 物理金相卷（总主编桂立丰，卷主编唐汝钧，辽宁科学技术出版社，
沈阳，1999年11月第1版），第三篇，第7章。
[4] Bourniquel B , Feron J . Proc. 1st Int. Conf. on Residual Stresses, DGM  Informations  gesellschaft .1987. 275
[5] 徐寒冰，盖秀颖，宋小平，李家宝，理化检验，物理分册，34（7），1998，16.
[6] 中华人民共和国国家标准GB7704-87《X射线应力测定方法》。
[7] 白岩俊男，阪本喜保. X射线应力测定标准方法附录五.
[8] B. D. Cullity. Elements of X-ray diffraction. Addison-Wesley Publishing Company, Inc.  Reading, Massachusetts,U. S. A.  London, England. 157.
[9] 何家文. 提高淬火钢X射线应力测定准确度（兼评平行光束法）。西安交通大学科学技术报告. 1975.
[10] 冉启芳,李家宝,何家文. X 射线衍射学进展（许顺生主编，科学出版社）第七章，X射线应力测定技术的进展: 243
[11]  王仁智.金属学报.1982,18(4):493-500
[12]  袁发荣,伍尚礼.残余应力测试与计算.长沙:湖南大学出版社,1987.
[13]  杨于兴,漆玄. 金属X射线衍射分析.上海交通大学.